Spearman’s correlation in statistics is a nonparametric alternative to Pearson’s correlation. Use Spearman’s correlation for data that follow curvilinear, monotonic relationships and for ordinal data. Statisticians also refer to Spearman’s rank order correlation coefficient as Spearman’s ρ (rho).
In this post, I’ll cover what all that means so you know when and why you should use Spearman’s correlation instead of the more common Pearson’s correlation.
To learn more about correlation in general, and Pearson’s correlation in particular, read my post about Interpreting Correlation Coefficients.
Throughout this post, I graph the data. Graphing is crucial for understanding the type of relationship between variables. Seeing how variables are related helps you choose the correct analysis!
Related post: Nonparametric versus Parametric Analyses
Choosing Between Spearman’s and Pearson’s Correlation
Let’s start by determining when you should use Pearson’s correlation, which is the more common form. Pearson’s is an excellent choice when you have continuous data for a pair of variables and the relationship follows a straight line. If your data do not meet both of those requirements, it’s time to find a different correlation measure!
The data in the graph have a correlation of 0.8. Pearson’s correlation is valid for these data because the relationship follows a straight line.
Consider Spearman’s rank order correlation when you have pairs of continuous variables and the relationships between them don’t follow a straight line, or you have pairs of ordinal data. I’ll examine those two conditions below.
Why Pearson’s correlation is not Valid for Curvilinear Relationships
The graph below shows why Pearson’s correlation for curvilinear relationships is not valid.
On the graph, the data points are the red line (actually lots and lots of data points and not actually a line!). And, the green line is the linear fit. You don’t usually think of Pearson’s correlation as modeling the data, but it uses a linear fit. Consequently, the green line illustrates how Pearson’s correlation models these data. Clearly, the model doesn’t fit the data adequately. There are systematic (i.e., non-random departures) between the red data points and green model fit. Right there, you know that Pearson’s correlation is invalid for these data.
The Pearson’s correlation is about 0.92, which is pretty high. However, the graph emphasizes how it does not capture the whole relationship. The real strength of the relationship is even higher. Later in this post, we’ll work through a similar example using scientific data.
Determining when to use Spearman’s Correlation
Spearman’s correlation is appropriate for more types of relationships, but it too has requirements your data must satisfy to be a valid. Specifically, Spearman’s correlation requires your data to be continuous data that follow a monotonic relationship or ordinal data.
When you have continuous data that do not follow a line, you must determine whether they exhibit a monotonic relationship. In a monotonic relationship, as one variable increases, the other variable tends to either increase or decrease, but not necessarily in a straight line. This aspect of Spearman’s correlation allows you to fit curvilinear relationships. However, there must be a tendency to change in a particular direction, as illustrated in the graphs below.
| Positive Monotonic: tends to increase but not necessarily in a linear fashion. |  |
| Negative Monotonic: Tends to decrease but not necessarily in a linear fashion. |  |
| Non-Monotonic: No overall tendency to either increase or decrease | 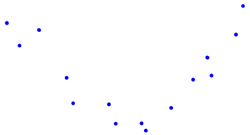 |
Spearman’s rho is an excellent choice when you have ordinal data because Pearson’s is not appropriate. Ordinal data have at least three categories and the categories have a natural order. For example, first, second, and third in a race are ordinal data.
For example, imagine the same contestants participate in two spelling competitions. Suppose you have the finishing ranks for all contestants in both matches and want to calculate the correlation between contests. Spearman’s rank order correlation is appropriate for these data.
Spearman’s rho is also a great way to report correlations between Likert scale items!
How to Calculate Spearman’s Rho
Spearman’s correlation is simply the Pearson’s correlation of the rankings of the raw data. If your data are already ordinal, you don’t need to change anything. However, if your data are continuous, you’ll need to convert the continuous data into ranks. Of course, many statistical software packages will do that preprocessing for you and simply calculate the answer!
The example dataset below shows data ranks for two continuous variables. The data are ranked such that a value of 1 indicates the highest, 2 the second highest, and so on.
To determine Spearman’s correlation, simply calculate the Pearson’s correlation for the two rank order columns instead of the raw data. We’ll analyze these data later in the post!
Learn how to calculate correlation in my post, Correlation Coefficient Formula Walkthrough.
Interpreting Spearman’s Correlation Coefficient
Spearman’s correlation coefficients range from -1 to +1. The sign of the coefficient indicates whether it is a positive or negative monotonic relationship. A positive correlation means that as one variable increases, the other variable also tends to increase. A negative correlation signifies that as one variable increases, the other tends to decrease. Values close to -1 or +1 represent stronger relationships than values closer to zero.
Comparing Spearman’s and Pearson’s Coefficients
If the Pearson’s coefficient is a perfect -1 or +1, Spearman’s correlation coefficient will be the same perfect value unless there are repeating data values.
| Correlation of +1 for both Spearman’s and Pearson’s correlations |  |
| Correlation of -1 for both Spearman’s and Pearson’s correlations |  |
When there is no tendency for two variables to change in tandem, both Spearman’s and Pearson’s will be close to zero, indicating no relationship.
If there is a curvilinear but non-monotonic relationship, both Spearman’s and Pearson’s correlation will be close to zero.
However, when you have two variables with a curvilinear, monotonic relationship, you’ll find that Spearman’s correlation indicates a stronger relationship (rho has a higher absolute value) than Pearson’s. In those cases, the curvilinear nature “confuses” Pearson’s, and it underestimates the relationship’s strength. The upcoming example illustrates this aspect in action.
Spearman’s Correlations for Likert Items and Other Ordinal Data
Statisticians report correlations of ordinal data, such as ranks and Likert scale items, using Spearman’s rho. Strongly positive Spearman’s correlations indicate that high ranks of one variable tend to coincide with high ranks of the other variable. Negative correlations signify that high ranks of one variable frequently occur with low ranks of the other variable.
For Likert items using the Strongly Agree to Strongly Disagree scale, Spearman’s correlations mean the following:
- Strongly positive coefficients: Strongly Agree values tend to occur together.
- Strongly negative coefficients: Strongly Agree for one item is apt to coincide with Strongly Disagree on the other item.
- Near zero coefficients: The value of one Likert item does not predict the other Likert item’s value. There is no relationship between them.
Related post: Analyzing Likert Scale Data
Example of Spearman’s Rank Order Correlation for a Monotonic Relationship
The graph below displays the relationship between density and electron mobility. The relationship is nonlinear. In fact, I fit a nonlinear regression model to these data. However, instead of fitting a regression model, let’s calculate the correlation between these two variables. These data are a good candidate for Spearman’s correlation because they follow a nonlinear relationship that is monotonic. As Density increases, electron mobility also increases., but not in a linear fashion.
These data are freely available from the NIST and pertain to the relationship between density and electron mobility. Download the Excel data file to try it yourself: ElectronCorrelations.
I’ve done the calculations in Excel so you can see how they compare. Excel’s Data Analysis ToolPak performs Spearman’s correlation. It doesn’t explicitly calculate Spearman’s correlation. However, by using Excel’s rank function to rank both variables, I can then use Pearson’s correlation on those ranks to derive Spearman’s rho.
First, I’ll calculate Pearson’s correlation.
The correlation is a very strong ~+0.96. Despite being nonlinear, Pearson’s indicates it is a strongly positive relationship. However, despite being a high correlation, we know that it underestimates the strength because it can’t model nonlinear relationships.
Now, let’s calculate Spearman’s rho. In the Excel spreadsheet, I used the rank function to convert the raw scores for both variables to ranks. Then, I calculated the correlation for the pair of ranked values to produce Spearman’s rho.
Related post: Using Excel to Calculate Correlation
For the electron mobility data, Spearman’s rho is a near perfect correlation of +0.99. It’s nearly perfect because these data represent a physical process and the lab collected extremely precise measurements.
Spearman’s correlation is a great addition to your statistical toolbox! It allows you to calculate correlations for data where Pearson’s is invalid. While Spearman’s correlates ranks, the Mann Whitney U test compares the average ranks of two groups.









Hi Jim
With Spearman’s test, when calculating sample size (n), do you include data from participants with a zero difference between the ranks of their scores for the two variables?
Thanks
Mark
Hi Mark,
When using Spearman’s rank correlation coefficient to assess the relationship between two variables, the primary focus is on the rank order of the scores rather than their absolute values.
Zero differences represent tied data, and you should include those in the analysis. Typically, statistical software gives tied data an average rank for each set of tied scores. Including ties ensures that the coefficient represents the relationship for all values in the dataset. Hence, these data points count towards the sample size.
Dear Jim
Thank you for your wonderful writings. I have one question regarding canonical correlation. How to correlate a group of variables with another group for the Likert-scale. My further questions are
1. Can we group the variables into factors using Median, then correlate the factors?
2. Can we use canonical correlations for Liker scale data when the data are not normally distributed?
Thank you.
Hi Nguyen,
Your proposed canonical correlation analysis (CCA) is atypical. Because I don’t understand exactly what you are doing and why by grouping variables into factors using the median and how your unusual approach affects the results, I’m hesitant to provide guidance.
Typically, CCA uses raw data values. I’m not sure the impact of grouping variables by using the median or even exactly what you mean by that.
There is an assumption of multivariate normality between the two canonical variables. I’m unsure about the severity of violating that assumption. Because you’re using Likert scale data, it seems like it’s likely a problem. It almost seems like you’d need a CCA variant that uses Spearman’s correlation but I’m not even sure that exists!
In short, I don’t have expertise specifically in CCA and your method is unusual, so I don’t want to give any incorrect advice. I’d suggest contacting a statistician who is more familiar with CCA specifically and can dedicate the time to seeing how it applies to your specific study.
Best of luck with your interesting project!
I have a question about when to use Pearson and when to use Spearman. I have two variables. One is skewed and kurtotic and the other is skewed. Would I use Spearman for this correlation analysis? I enjoy your explanations and appreciate your help.
Hi Melody,
It really depends on the nature of the relationship between the variables. From the distributions you describes, it sounds likely that you’d use Spearman’s. But you should graph the data in a scatterplot to be sure. If the relationship forms a straight line, Pearson’s is probably a good choice. If it’s curved, probably use Spearman’s. Although, as I show in this post, Spearman’s doesn’t work for all curved relationships. So, graph the data and use that to make the decision.
Hi Jim,
The last question has me thinking about my results. I have negatively skewed data, which I assume contributes to my negative coefficient values. Is that a correct assumption? I’m trying to figure out what to do with the many 0 scores for participants not interested in taking action. If I counted 0 as missing data instead of a valid score, the results would differ. For context, I am comparing a computed score of activities one could participate in, with how much one feels about the issue. One measure is an ordinal, and the other interval – hence the use of Spearman’s rho. Also, I’m not sure how to do this.
Hi Peta,
If you’re talking about the distribution of a single variable, the skew is not related to the correlation coefficient value. In other words, a negative (left) skew for one variable’s distribution does not suggest that the correlation coefficient will be negative. A negative correlation coefficient indicates that above average values of one variable correspond with below average values of another variable. In your case, it relates to ranks rather than data values because you’re using Spearman’s correlation–which is appropriate for ordinal data. The negative correlation has nothing to do with the skew of either individual distribution.
I don’t know enough about your study or the subject area to make a suggestion about the zero scores. Removing subjects with zero scores because they are non-participants might be valid. But I can’t say for sure. I suggest you search the literature to see how similar studies handle this issue.
I hope this helps!
Hi Jim, I’m still a bit confused as to which one to use! I have data on an association between age and calcium levels, but the data is slightly skewed and has some outliers. I assumed that would mean I should use spearman but my data doesn’t look monotopic? It doesn’t increase or decrease it’s mainly scattered in a straight horizontal line. Would appreciate any help!
Hi
If it’s a horizontal line, that suggests there’s no relationship between the variables. As age increases, there’s no tendency for calcium levels to increase or decrease.
Spearman’s is the safe choice in terms of satisfying assumptions. A slight skew isn’t necessarily a showstopper for Pearson’s particularly when you have a decent sample size. The outliers might be a problem. You can try Pearsons with and without the outliers to see if they make much of a difference.
The most important thing to look for on the graph is whether you can fit a straight line through the data points on the graph. If you can, Pearson’s is probably ok. If not, you might need a different method, such as Spearman’s. From your description, it sounds like you can fit a straight line, although unfortunately if it’s roughly horizontal, the correlation will be close to zero.
There are only parametric vs. non-parametric analyses, but not distributions. What do you mean?
Hi Jim,
If I had two ordinal variables, what would be the benefit of using a correlation test instead of a chi-square one, please? Would it be that a correlation can tell us the direction of any relationship whereas a chi-square test would not be able to tell us this?
Thanks.
Hi Charlotte,
Yes, that’s correct. A correlation test can tell you the direction and strength of the relationship between two ordinal variables along with a p-value for determining statistical significance, whereas a chi-square test can only tell you whether there is a statistically significant relationship between the two variables.
Spearman’s correlation is a good choice for two ordinal variables.
Conversely, chi-square is a test statistic that only leads to a p-value, allowing you to determine statistical significance. Is there a relationship or not? Chi-square will tell you if there is a statistically significant relationship, but it does NOT tell you the nature of the relationship. There is nothing directly equivalent to a correlation coefficient. You can compare cell values and look at which cells contribute to the most to the chi-square value to tease some of that information out. For an example, read my post about an example of the chi-square test of independence.
Typically, you’d follow significant chi-square test results with a separate assessment to evaluate the nature of the relationship, such as Cramer’s V. Many of those types of assessments have differing limitations and they’re not always straightforward. However, you’d usually use this approach for categorical variables and not ordinal variables.
Because you have ordinal variables, I’d just stick with Spearman’s correlation. One stop shopping for both the correlation coefficient and p-value. And understanding Spearman’s correlation coefficient is simply more informative.
I hope this helps! 🙂
Hello Jim,
Thanks for your excellent article on correlation analysis.
I have a problem.
What analysis test should I use when the two variables I am assessing have a parametric and a non-parametric distribution, respectively? I am confused about it.
Hi Jim that was really helpful. I misspoke when I said Pearson’s I am actually using a linear regression analysis to look at the interaction term. I have not looked at the residuals, I will! but just plotting the data look like the fits are reasonable (when I treat the ordinal data as continuous data which is what I’ve done for those regression analyzes.) I’m analyzing graduate teaching assistant data from midterm evaluations by students. And there’s one question that scores the overall ta rating and then there’s a bunch of other questions that are specific to certain behaviors. And I’m interested in whether there are differences in the response for female Tas versus male Tas for different questions. So the regression analysis uses the overall ta score, treated as a continuous variable, as the Y and uses the categorical variable ta gender as one of the independent variables and also one of the specific questions that I’m looking at and then I put in the interaction term between that categorical and continuous variable to see if there’s a significant difference in the slope of those lines for males and females. I think I will reach out to the statistician. I do really appreciate your feedback about multiple analyzes of the same data set in one manuscript!
best
celia
Hi Celia,
That sounds like a good approach. You’ll need to be extra careful about checking those assumptions/residual plots because it can be harder to get a good fit with ordinal IVs.
Also, because you’re using an ordinal variable as the dependent variable, you should try ordinal logistic regression, because that’s designed for ordinal DVs. You can still fit the other variables and interaction term.
And, if you can’t get a good fit using the ordinal IV as a continuous IV, try including it a categorical IV.
But it sounds like you’re using a reasonable approach.
Hi Jim, thank a clear review. Great article. I wonder if you could make a suggestion for me. I’m working on a manuscript that is examining five Point likert scale data. The correlations are both monotonic and quite linear but I’ve used the spearman’s because it’s appropriate for ordinal data. What I think I remember , and I’m pretty sure is true, is that there’s no way to look at interaction terms between regression lines using non parametric corr.
But I have a reason to also want to know the interaction terms between two different groups looking at the same correlation, and it would help me answer important questions for the research.
I know that there are many people who do default to Pearson’s as long as their ordinal data are reasonably “continuous” and relationships monotonic. So, ultimately my question is I want to report the Spearman correlation coefficients because I think they’re the most appropriate, but then I also want to run the analysis using Pearson’s so that I can get those interaction terms and I want to share those as evidence for one of the questions. And I’d like to rationalize that by just talking about why I made those choices. I did speak to a statistician at the University about this but it didn’t seem like they thought it was usual to put two different ways to analyze the same data set into a research methodology. To me it seems like the right thing to do and also the only way to answer the questions that I want to answer in the most honest way possible.
Can you share your knowledge and advice and experience on this particular set of questions?
Best
Celia
Hi Celia,
For starters, I think it’s ok to show different types of analysis in one study. You could include a discussion in your manuscript about why you chose to use both the Spearman and Pearson coefficients and explain the implications of using each method for your data and research questions. It is always important to be transparent and thorough in your methodology, and to provide a clear rationale for your decisions.
However, neither type of correlation is good for analyzing interactions because they don’t use a model that can assess interaction effects. Try using regression analysis to model the interaction. Likert data (and ordinal data generally) can be difficult to include as independent variables. You’ll need to include them either as continuous variables or as categorical variables. Either way, you can model the interaction term. But each approach has their pros and cons.
When you can get an adequate, unbiased fit using them as continuous variables, that is generally preferable. But sometimes that is not possible, particularly with Likert (and ordinal) data. You’ll need to check the residuals and other assumptions to be sure.
Alternatively, you can include them as categorical variables. It’s easier to get an unbiased fit using this approach, but it uses many more degrees of freedom, which can be problematic depending on your sample size and number of variables. However, this approach can be good when you can’t get an acceptable fit using them as continuous variables.
You might need to discuss how to model the interaction with the statistician. Likert data makes this a bit trickier!
Hi Jim
Please how do I calculate correlation using likert scale of 5 scale manually without using SPSS
If u can help with an example it will be well appreciated and understandable
Thanks, expecting a response please
Dear Jim,
Thank you so much for your valuable post.
I am not good at statistics but I need to do some of it for my study.
I conducted a questionnaire survey using likert 5 scale. I ran a spearman correlation analysis using spss and got results very different from what I expected. The majority of respondents answered “important” and “very important” for one variable and “Agree” and “Strongly Agree” for another variable. Yet the Spearman’s rho from the analysis results is 0.042 and p value is 0.454 respectively. I am confused if I have done the right way. Could you please help me with this?
Best regards,
Kim Pi
Hi Jim, thank you for the detailed article!
I am currently looking to correlate up to 40 different sets of data to each other, some of these data sets are normally distributed, and some not normally distributed.
I have tried to log10 the data however some data is still not normally distributed following the calculation.
Would the Spearman’s rho still be appropriate when comparing normally distributed data to not normal data?
My Likert scales have one IV and one DV as Ordinal, one is a 5-point scale and one is a 4-point scale. Would a correlation method of analysis be appropriate to determine if there is a relationship or the tendency of the data points to increase or decrease? If I changed the 4-point scale to a 5-point scale of Strongly Disagree (1), Disagree (2), Neutral (3); Agree (4), Strongly agree (5). would this be better? What type of analysis test would be best for one independent variable and one dependent variable?
Hi Debarah,
With two variables, yes, using Spearman’s correlation is a good option. You could also present the two variables in a contingency table and then use a chi-square test of independence to determine whether the relationship is significant. But Spearman’s correlation is probably sufficient.
Hi Jim,
Thanks for your article, it was really helpful. I was wondering if you can help me with the following question. When using Spearman correlation test, do you also have to calculate Rsquared, the coefficient of determination? I’ve read that because is a ranked correlation, the result, rho, is enough to conclude not only about the direction but also for the strength of the correlation. So, apart from the p-value and the rho, is Rsquared also important for Spearman’s correlation?
Thank you!
Maria
Hi Jim,
I am running statistical tests on the correlation between gender, age, education level and living area (rural or urban) for data I have collected for my dissertation. I have used Spearman’s Rank correlation and have got weak rho values (such as -0.09 and 0.053), but have been getting high p-values (such as 0.520, 0.293 and 0.950). Please could you help me in understanding how to interpret these results?
Many thanks,
Jess
Hi Jess,
The correlation values indicate that there is virtually no relationship between your pairs of variables. Additionally, the high p-values indicate that your results not significant. In other words, you cannot conclude that the correlation coefficients are different from zero (no effect). I’m sorry to say but the results do not show that a relationship exists between your variables in the population.
Thanks Jim, I really enjoyed reading this post
Hi Jim,
Thanks for all the work you do with these explanations! I have two scales measuring depression, and each is 21 items. The ranges for scoring are different, however: e.g., Scale 1 has 0-9 = normal, 10-13 mild, etc., whereas Scale 2 has 0-13 = minimal, 14-19 = mild, etc. I’m having a bit of trouble figuring out how to compute these to get the correlation between the two scales. For example, if I would convert the category into a numerical value (eg normal = 1, mild = 2) and then average those values, or if I would get a total score for each scale and then use those for the correlation.
Best,
(also) Jim
Hi Jim,
I’m a high school junior learning statistic from you for my science fair project. I studied radon gas emission and found a correlation between radon, temperature, and humidity to be clearly represented on my graphs. I learned that I should be using the Spearman’s correlation because of the distribution of the data (non-linear). Luckily I can pull-up the Coefficient, N, T statistic, DF, and p value using the formula in Excell- I’m just having a hard time interpreting the data. My critical probability value is 0.0268. Since this is less than 0.05 does this mean that there is a significant correlation between the data? Should a null hypothesis follow this analysis if I’m making an inference about radon in my whole neighborhood based on 12 samples? Thanks for your help!
CP
Hi Connor,
That’s a great use for statistics!
You’re right that Spearman’s correlation is good for certain types of curvature. I show some of that in this post so you can see examples of what types of curves are OK and which ones aren’t (e.g., U or inverted U-shapes).
Yes, using a hypothesis test is good after this type of analyses. You’ve seen a relationship in your sample data. Now, if you want to use your sample to determine whether those relationships exist in the population, you need to use a hypothesis test. You see them in the sample, but they might not exist in the population. That’s where hypothesis tests come in. They help you determine whether your sample evidence is strong enough to conclude that the relationships exist in the population rather than just a sampling fluke.
If you can post your correlation coefficients and p-values (if you know them), I could discuss them in more detail. If you don’t know the p-values, please include your t statistics. When you have a p-value, you don’t need to interpret the t-statistic or the critical value.
The hypothesis test and its p-value take your sample size (n) into consideration. So, sample size is a factor in the analysis, but you don’t need to worry about doing anything with the number. It’s customary to report the sample size with your results. But you don’t need to interpret the value.
DF is the degrees of freedom. It’s another factor in the analysis but the test factors that in. You don’t need to interpret it or present the number in the results. If you want to learn more about DF, you can read my post about degrees of freedom.
I hope that helps. If you can share the other results, I can help you interpret them further.
Hi Jim,
Thanks for the very clear explanation.
I have a question about supporting tests.
In my research project, I have a model that generates an expected (deterministic) order of set items (n=16). From fieldwork observations, I also have the actual observed rank order list (n<=16, there may be instances where one of the expected cases is not observed). However, there will be no observations that are not in the expected list (I believe this is "conjoint"). I use Spearman's rank order correlation to test the monotonic relationship.
I initially also ran ordinary least squares regression on the pairs and then tested the residuals for normality and randomness, but now realize that is probably not the correct handling for ordinal data.
My question is are there other tests that I should run on these paired lists? Tests for normality or randomness? I know Spearman's is a non-parametric test, but what would bolster the validity of my Spearman's results, if anything?
Dave
Hi Dave,
You might try performing ordinal logistic regression if you have a set of potential predictors. Use your rank order list as the dependent variable. Although, your sample size is very small (n=16), so you might be able to include one predictor, but you’ll be very limited by the sample size.
You can’t test for normality with ordinal data. While you know the order, the differences between adjacent observations might not be consistent.
You could perform a nonparametric test to determine whether the medians of your two groups are different. If I understand correctly, you have a list of actual vs. expect rank-orders. You might want to show that there is no significant difference between the medians. Maybe? Although, a lack of significance can be due to the small sample size rather than true equivalence.
I don’t understand your context or what you want to learn, so it’s difficult to answer. But those are several possibilities.
Hi this explanation has been really useful, I am new to quantitative methods and have been using spss for the first time. My data set is based on a survey that used likert scales, and I am looking at the relationship between stress at work and impact on homelife. Spearmans rho test has shown a positive correlation. what I wanted to know if I were to further look at the data and look at differences between these associations and gender would I just look at the data separately or would I have to do a different test.
Hi Marriam,
To look at the differences between genders, you’d need to use a 2-sample hypothesis test. With Likert data, which is ordinal rather than continuous, there is some debate over whether you can use the 2-sample t-test to compare means or a 2-sample nonparametric test to compare medians. I write a post about how to analyze Likert data where I reference research suggests that either is appropriate.
Thank you for this valuable post.
I woudl like ask about monotonic. How can I know if it is a monotonic or linear in order to know wheather I have to use Pearson or Spearman?
Also, if I have an outlier and/or the data is not normal distributed, then which one is the correct one to use? In other words, what are teh requirments to apply Pearson and Spearman?
Thank you in advanced
Hi Weam,
There are two things to consider for correlation when it comes to assumptions. One is for the correlation coefficient and the other is for the p-values associated with the coefficient. The p-value assumptions are somewhat more stringent than for the correlation coefficient itself.
For the correlation coefficients, it’s largely the shape of the relationship that matters. If the paired data generally follow a straight line (i.e., the variables change together and at an overall constant rate), then you can use Pearson’s correlation. However, if is a tendency for the variables to change together but the rate is not constant (i.e., some curved relationships), then you have monotonic relationship. I cover that in this post. For monotonic relationships, you can use Spearman’s correlation.
To trust the p-values for these correlation coefficients, you need to consider the distribution of values. Technically, you need a bivariate normal distribution to use Pearson’s correlation to be able to trust the p-value. However, like many tests, the p-values for Pearson’s correlation are robust to departures from normality when you have a sample size greater than ~25.
I’m not entirely sure about the assumptions for the Spearman’s p-values, but I believe they are the same because the use the same underlying methodology.
So, keep in mind that the assumptions for using either method to get the correlation coefficient is largely based on the shape of the relations. Or, if you’re using ordinal/ranked data, use Spearman’s. And that there are additional requirements to trust the p-values, but those can be waived with a large enough sample size.
Hi Jim
Thanks for writing such an interesting articles, I really enjoy reading them and learn a lot too.
I am here with a question that is it ok to do correlation with data points as low as 5? For example, I expose my model organism to different doses in replications and see how many of these organisms die during the entire period of their development to a particular stage? I am meausring development in terms of days. I observe that individuals in each treatment and even in different replications of same treatment respond differently. Like in case of treatment 1, There are few mortalities occuring in replication 1 but not in replication 2 and 3 on the same day. same kind of response was observed throughout the experiment. Now I am interested to find out whether the mortalities occuring due to ingestion of contaminant and therefore thinking of correlation. I have divided my data with respect to treatment and each treatment includes the mortalities occuring on different days (irrespective of replication). I have data points for each treatment like this: day 1, 2% mortalities in Replication2, number of particles ingested 3 (data point 1), Day2, no mortalities, no ingestion, day 3, 16% mortalities in replication 1, ingestion of particles in replication 1= 14 particles (data point2), 18% mortality in replication 2 and ingestion of particles= 9 particles (data point 3), day 5 20% mortalities in replication 1, ingestion of particles in replication 1= 11 particles (data point4). Correlation between mortality and ingestion with 4 data points, is it ok? Regression between mortality and ingestion with 4 data points, is it ok? I am making a scatter plot of this,
Hi Rabia, that’s too few points for correlation. I suppose you could use it as a preliminary result, but it’ll be hard to obtain any meaningful insight from so few data points. If you try it, I’d recommend calculating a confidence interval for the correlation coefficient. That will tell you the uncertainty of the estimate. You will probably have a relatively wide CI. However, it’s possible that you might glean some insight from it. At least you’d understand the limitations of the estimate.
As for regression, you really need at least 10 observations for one IV. Ideally 15 or 20 for the first IV. Read my post about overfitting regression models to understand why you need a minimum number of observations per coefficient estimate and how many you need.
I’m wondering if you should be using Poisson regression (or negative binomial) because your DV is a count. Read my post about choosing the type of regression to learn more and look near the end of it for a section on count variables.
Thank you very much, Jim, your reply was very helpful, supportive and quick!
All the best,
Ivana
Hi Jim,
The article was very clear and easy to understand, thank you!
But still, I am struggling with the interpretation of my findings based on Spearman’s Rho correlation analyses. I am analyzing the employee survey data which are quite complex. The correlations between my variables range from about 0.17 to 0.5 (for positive correlations), not higher, but with the p-values of about 0.001 or even 0.000. The ordinal variables being analyzed are compound synthetic variables created by summing up several dichotomic variables that represent one topic (such as “trust”; “rivarly”, etc.). Normally, according to what I read in statistics manuals, the 0.4 correlation should be considered weak. On the other hand, in case you study mutifactorial social phenomena, I am afraid that the chance of getting a 0.7 correlation is very low. My question is whether the correlation coefficients should be always interpreted in the same way, or whether the researcher should consider the complexity of the matter they are correlating and under certain circumstances they could say that – let’s say – even a correlation of 0.3 means there is a relationship. What words should then one use to describe such correlations (0.2, 0.3, 0.4, 0.5)? The problem is that even the low correlations I got all make sense (they are in line with the theory and with the common sense).
Thank you very much for any help!
Hi Ivana,
Generally speaking, those correlations are considered weak. However, I’m not a big fan of rules for classifying whether a correlation is weak, medium, or strong because they vary so much by subject area. For example, if you’re measuring physical phenomenon, such as the electron mobility example in this article, an extremely high correlation is normal. However, if you’re measuring psychology attributes, correlations are going to be much lower.
So, a lot of the descriptive words about the strength of the correlations will depend on your field. It sounds like you’re more on the psychology side of things. I’d look at similar studies and see how they phrase the strength of similar correlations. See what correlations are typical and how yours compares. From my understand, I’d agree that correlations of 0.7 are unlikely, but it’s not really my field. So, I don’t want to say definitively how I’d describe, but look at similar studies and see how yours fits in.
While I wouldn’t describe them as overly strong they might well be consistent with other studies. Additionally, your significant p-values suggest that the correlations exist (i.e., do not equal zero) in the population. So, that’s a good thing! From what you write, and the bit I know about your field, I don’t see any glaring issues. If the correlations make theoretical sense and they’re significant, it’s sounding pretty good!
Dear Jim,
Thank you for wondefule explanation of Correlation.
My question is when we use Pvalue less than 0.01 and when P value less than 0.05?
Thank you in advance for your time
Warm regards NB
Hi Negin,
I’m so glad you found it to be helpful!
For your question, I’ve written a blog post about that! You’re actually asking about the significance level (alpha), to which you compare the p-value. Click the link below to read a post where I explain the significance level and how to choose between 0.05, 0.01, and even 0.10!
Understanding Significance Levels
Dear Jim!
Many thanks for the quick reply that helps a lot!
All the best,
Rainer
You’re very welcome, Rainer! 🙂
Thanks Jim Frost but I have one questions do you have the books about Spearman’s correlation
Dear Jim,
I have a question concerning the use of Spearman’s correlation for test-restest reliability. I have clearly ordinal data and conducted a CFA with unweighted least squares which seems appropriate for it. Then I calculated oridnal versions of Cronbach’s Alpha and McDonald’s Omega as measure of internal consistency and everything worked fine. But then I was wondering how to assess test-retest reliability for ordinal data. Publications covering this topic seem scarce, therefore, it would be very helpful to hear your expertise on this topic. Many thanks in advance for any help!
All the best,
Rainer
Hi Rainer,
Yes, it sounds like Spearman’s rho is a good way to assess test-retest reliability for your data.
Thanks, Jim, that’s a good refresher on using Spearman’s rho. In the example, what if the midsection of the graph (roughly between density of 200 and 1200 is not monotonic, but mostly horizontal (with some scatter) instead? Or if the midsection dips downward? How would that affect Spearman’s rho?
Hi Jeremy,
The key point with Spearman’s is the tendency of the data points to increase or decrease on an overall basis for a dataset. Imagine a dataset we sort the X-Y pairs based on the ascending X values. If we go down the list of increasing X values and notice that each subsequent Y value is always higher than the previous Y, Spearman’s rho is +1. It doesn’t matter how much each Y increase from one to the next as long as each subsequent Y is higher than the previous Y when sorted by X. There are many different shapes that describes. You get the perfect correlation because the ranks for X and Y perfectly agree.
Now, on to your question. What I write above almost describes the electron mobility data. There are a few ranks that are out of order, which is why we have a near but not perfect +0.99. If you fiddle with the middle of the distribution so it flattens or dips, you’ll have more ranks that don’t perfectly align. The result would be a lowering of Spearman’s rho. How much depends on how many ranks are not aligned perfectly.
How can i buy hard Copy of the text book?
Hi Elijah,
Yes, you definitely can! You can get them from Amazon. Go to My Webstore for the Amazon links by country. You can also find them for order from other online retailers. Many physical bookstores can also order copies for you.
you have simplified particularly on when to use.