Inferential statistics lets you draw conclusions about populations by using small samples. Consequently, inferential statistics provide enormous benefits because typically you can’t measure an entire population.
However, to gain these benefits, you must understand the relationship between populations, subpopulations, population parameters, samples, and sample statistics.
In this blog post, learn the differences between population vs. sample, parameter vs. statistic, and how to obtain representative samples using random sampling.
Related post: Difference between Descriptive and Inferential Statistics
Populations
Populations can include people, but other examples include objects, events, businesses, and so on. In statistics, there are two general types of populations.
Populations can be the complete set of all similar items that exist. For example, the population of a country includes all people currently within that country. It’s a finite but potentially large list of members.
However, a population can be a theoretical construct that is potentially infinite in size. For example, quality improvement analysts often consider all current and future output from a manufacturing line to be part of a population.
Populations share a set of attributes that you define. For example, the following are populations:
- Stars in the Milky Way galaxy.
- Parts from a production line.
- Citizens of the United States.
Before you begin a study, you must carefully define the population that you are studying. These populations can be narrowly defined to meet the needs of your analysis. For example, adult Swedish women who are otherwise healthy but have osteoporosis.
Population vs Sample
It’s virtually impossible to measure a whole population completely because they tend to be extremely large. Consequently, researchers must measure a subset of the population for their study. These subsets are known as samples.
Typically, a researcher’s goal is to draw a representative sample from their target population. A representative sample mirrors the properties of the population. Using this approach, researchers can generalize the results from their sample to the population. Performing valid inferential statistics requires a strong relationship between the population and a sample.
In a later section, you’ll learn about the importance of representative samples and how to obtain them.
A statistical inference is when you use a sample to infer the properties of the entire population from which it was drawn. Learn more about making Statistical Inferences.
Learn more in-depth about Populations vs. Samples: Uses and Examples and Sample Mean vs. Population Mean.
Subpopulations can Improve Your Analysis
Subpopulations share additional attributes. For instance, the population of the United States contains the subpopulations of men and women. You can also subdivide it in other ways such as region, age, socioeconomic status, and so on. Different studies that involve the same population can divide it into different subpopulations depending on what makes sense for the data and the analyses.
Understanding the subpopulations in your study helps you grasp the subject matter more thoroughly. They can also help you produce statistical models that fit the data better. Subpopulations are particularly important when they have characteristics that are systematically different than the overall population. When you analyze your data, you need to be aware of these deeper divisions. In fact, you can treat the relevant subpopulations as additional factors in later analyses.
For example, if you’re analyzing the average height of adults in the United States, you’ll improve your results by including male and female subpopulations because their heights are systematically different. I’ll cover that example in depth later in this post!
Parameter vs Statistic
A parameter is a value that describes a characteristic of an entire population, such as the population mean. Because you can almost never measure an entire population, you usually don’t know the real value of a parameter. In fact, parameter values are nearly always unknowable. While we don’t know the value, it definitely exists.
For example, the average height of adult women in the United States is a parameter that has an exact value—we just don’t know what it is!
The population mean and standard deviation are two common parameters. In statistics, Greek symbols usually represent population parameters, such as μ (mu) for the mean and σ (sigma) for the standard deviation.
A statistic is a characteristic of a sample. If you collect a sample and calculate the mean and standard deviation, these are sample statistics. Inferential statistics allow you to use sample statistics to make conclusions about a population. However, to draw valid conclusions, you must use particular sampling techniques. These techniques help ensure that samples produce unbiased estimates. Biased estimates are systematically too high or too low. You want unbiased estimates because they are correct on average.
In inferential statistics, we use sample statistics to estimate population parameters. For example, if we collect a random sample of adult women in the United States and measure their heights, we can calculate the sample mean and use it as an unbiased estimate of the population mean. We can also perform hypothesis testing on the sample estimate and create confidence intervals to construct a range that the actual population value likely falls within. Learn more about Parameters vs Statistics.
The law of large numbers states that as the sample size grows, sample statistics will converge on the population parameters. Additionally, the standard error of the mean mathematically describes how larger samples produce more precise estimates.
| Population Parameter | Sample Statistic |
| Mu (μ) | Sample mean |
| Sigma (σ) | Sample standard deviation |
Related posts: Measures of Central Tendency and Measures of Variability
Representative Sampling and Simple Random Samples

In statistics, sampling refers to selecting a subset of a population. After drawing the sample, you measure one or more characteristics of all items in the sample, such as height, income, temperature, opinion, etc. If you want to draw conclusions about these characteristics in the whole population, it imposes restrictions on how you collect the sample. If you use an incorrect methodology, the sample might not represent the population, which can lead you to erroneous conclusions. Learn more about Representative Samples.
The most well-known method to obtain an unbiased, representative sample is simple random sampling. With this method, all items in the population have an equal probability of being selected. This process helps ensure that the sample includes the full range of the population. Additionally, all relevant subpopulations should be incorporated into the sample and represented accurately on average. Simple random sampling minimizes the bias and simplifies data analysis.
I’ll discuss sampling methodology in more detail in a future blog post, but there are several crucial caveats about simple random sampling. While this approach minimizes bias, it does not indicate that your sample statistics exactly equal the population parameters. Instead, estimates from a specific sample are likely to be a bit high or low, but the process produces accurate estimates on average. Furthermore, it is possible to obtain unusual samples with random sampling—it’s just not the expected result.
Procedures for collecting a representative sample include the following probability sampling methods:
Additionally, random sampling might sound a bit haphazard and easy to do—both of which are not true. Simple random sampling assumes that you systematically compile a complete list of all people or items that exist in the population. You then randomly select subjects from that list and include them in the sample. It can be a very cumbersome process.
Random sampling can increase the internal and external validity of your study. Learn more about internal and external validity.
Conversely, convenience sampling does not tend to obtain representative samples. These samples are much easier to collect but the results are minimally useful.
Let’s bring these concepts to life!
Related post: Sample Statistics Are Always Wrong (to Some Extent)!
Example of a Population with Important Subpopulations
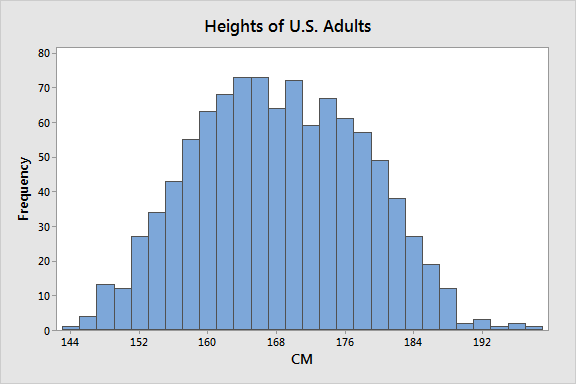
Suppose we’re studying the height of American citizens and let’s further assume that we don’t know much about the subject. Consequently, we collect a random sample, measure the heights in centimeters, and calculate the sample mean and standard deviation. Here is the CSV data file: Heights.
We obtain the following results:
Because we gathered a random sample, we can assume that these sample statistics are unbiased estimates of the population parameters.
Now, suppose we learn more about the study area and include male and female as subpopulations. We obtain the following results.
Notice how the single broad distribution has been replaced by two narrower distributions? The distribution for each gender has a smaller standard deviation than the single distribution for all adults, which is consistent with the tighter spread around the means for both men and women in the graph. These results show how the mean provides more precise estimates when we assess heights by gender. In fact, the mean for the entire population does not equal the mean for either subpopulation. It’s misleading!
During this process, we learn that gender is a crucial subpopulation that relates to height and increases our understanding of the subject matter. In future studies about height, we can include gender as a predictor variable.
This example uses a categorical grouping variable (Gender) and a continuous outcome variable (Heights). When you want to compare distributions of continuous values between groups like this example, consider using box plots. This plot become more useful as the number of groups increases.
This example is intentionally easy to understand but imagine a study about a less obvious subject. This process helps you gain new insights and produce better statistical models.
Using your knowledge of populations, subpopulations, parameters, sampling, and sample statistics, you can draw valuable conclusions about large populations by using small samples. For more information about how you can test hypotheses about populations, read my Overview of Hypothesis Tests.
When you take measurements, ensure that your measurement instruments and test scores are valid. To learn more, read my post Validity.




Thanks for your thoughtful response, Jim – I appreciate you taking the time.
That makes a lot of sense. To be crystal clear, and using the M&A hypothetical as an example, am I right in thinking that I would therefore need to use a hypothesis test in order to demonstrate any statistically significant year-on-year change in frequency/observations/count? i.e. establish that the annual samples are likely to come from different populations (say, rates of M&A activity) and are not different merely due to randomness/variation?
I think perhaps the all-too-common sensationalist interpretations in the financial media of year-on-year changes in activity without statistical testing have contributed to my confusion! Are there any grounds at all to compare a 2021 “population” of complete observations vs a 2022 population of observations, say, and coming up with a definite conclusion without statistical testing? Or are the media wrong to do so?
Thank you again – I appreciate my initial questions have spilled over into a second set, but this would really help clear things up for me! In the meantime, I’ve purchased a couple of your books, which look fantastic, and will enjoy improving my understanding in due course.
Best regards,
Kerry
Hi Jim,
Thanks for the great site.
With reference to the following statement, I was hoping you could kindly advise your position on the examples below.
“However, a population can be a theoretical construct that is potentially infinite in size. For example, quality improvement analysts often consider all current and future output from a manufacturing line to be part of a population.”
Ex1: How would you treat the performances of an athlete or sports team in any given year? Assuming all recorded performances are available, do they constitute a population or are they merely a sample of the athlete’s/team’s inherent ability?
Ex2: If we count all instances of an event in a given year (for example, the number of public M&A transactions worldwide), does this constitute a complete population, or merely a sample of all M&A transactions that could theoretically exist now and in the future?
Thank you very much in advance for considering my request.
All the best,
Kerry
Hello,
Thank you for your question and for the kind words about the site.
Ex1: In the case of an athlete or sports team’s performances, it depends on the context. If you’re considering the entirety of an athlete’s or team’s career, then the performance in a single year could be viewed as a sample because it does not encompass all the performances that the athlete or team has or will have. It’s a subset of a larger ‘population’ (the athlete’s or team’s overall career). However, if you are specifically interested in performance within a given year, then those performances could constitute a ‘population’ for that particular context or research question.
Ex2: Regarding the number of public M&A transactions in a given year, again it depends on your research question. If you’re studying M&A transactions within a specific year, then the transactions that occur during that year can be considered a ‘population’. However, if your scope of interest includes M&A transactions across multiple years or indefinitely into the future, then the transactions in a given year would be a sample of that larger, potentially infinite population.
In both cases, your sample or population is defined by the scope of your research question or area of interest. The distinction between a sample and a population isn’t a fixed, objective attribute of a set of data, but rather a perspective that depends on the particular context and research goals.
I hope this provides some clarity on your inquiry. Please feel free to ask if you have any further questions.
Best Regards.
hello jim, will you explain this statement?
“”The parameter is drawn by the measurements of units in the sample, and statistics is drawn by the measurements of the population”.
Hi Aileen,
I *think* I know that statement is trying to say but it’s not totally clear. The first part explains that you can use a sample to estimate the parameters of a population, such as the mean and standard deviation. Remember, inferential statistics will use a sample to infer the properties of a population. I write about that in this post. So, read that to understand that portion. The second part I’m not totally clear on what it’s trying to say. Typically, when you talk about “a statistic,” we’re referring to a value computed from a sample. Contrary to what the statement says, a statistic is NOT a measure from a population. Also, the use of the word “drawn” is unusual in that statement.
To understand what I believe this statement is trying to explain in a confusing and at least partially incorrect manner, read this post and also read my post about descriptive and inferential statistics.
how do u know if the standard deviation is stat or parameter?
Hi Noor,
If you’re using a sample drawn from a population (i.e., you didn’t measure the entire population), then you have a sample statistic, which is also known as a parameter estimate. However, if you measure the entire population (almost always impossible), then the value is the parameter itself. For example, if you measure the heights of everyone in population, the mean height is the population parameter.
However, you almost always work with sample statistics (parameter estimates) because you generally cannot measure the entire population.
population vs. sample, and the terms
parameter vs. statistic which a researcher almost always use, and
why?
Hi Hamthal,
Read this article more carefully! It’s clear in this article that researchers will almost never know the population parameters. In fact, they are usually unknowable. Instead, researchers use sample statistics to estimate the parameter values.
Hi Jim, if the only sampling method that we can use is convenience sampling ,or samples that are obtained by voluntary response (which are biased), should we still proceed with our research?
Hi Melissa
That’s a tricky situation. Often researchers will have samples that aren’t truly random. The question then becomes understanding the implications of the nonrandomness for your sample.
Are you talking about data that aren’t random but used a systematic technique such as a stratified or clustered sample? These methods approximate random sampling but use some intentional differences. I talk about these methods in my Introduction to Statistics ebook. There are techniques that can handle these types of samples.
Or, do you mean a convenience sample? In this case, you need to understand the ways in which your sample is different than your study population. Your results might be biased on way or another. There’s no firm answer I can give here because it depends on the specifics of how your sample is different from the population. It weakens your evidence undoubtedly. You can’t really trust the p-values and confidence intervals. Effects can biased. How much these issues affect your results depends on your sample. How different is your sample from a random sample? You need to understand that. A place to start would be to look at the various properties of your sample and compare those properties to published values of the population you are studying. Are there any striking differences?
I hope that helps!
Hello Sir
Does the value of statistic necessarily equal parameter and why?
Hi Yvonne,
It can be surprising, but no, the sample statistic doesn’t necessarily equal the population parameter. In fact, the sample statistic is almost always at least a little different from the parameter. That difference between statistics and parameter is sampling error. A key goal of inferential statistics is estimating the size of sampling error so you can understand how good your estimate is. Sampling error occurs because your sample, even with appropriate random sampling methodology, won’t exactly represent the full population.
For more on this topic, read my post about how sample statistics are always wrong (to some extent).
How bias influences the estimation of a population parameter
Such a helpful content ,understood the topic very clearly ,thanks uh so much sir for providing this kind of explanation
Extremely grateful !
–trusha
Hi therre. Is a population parameter a value or the characteristic? i.e. is the population parameter ‘the proportion of faulty items in a production batch’ or ‘5% of items in a production batch are faulty’
Thank you 🙂
Hi Allissa,
A parameter is a value that describes a characteristic of a population. For example, the mean height of all women in the United States is a parameter. It has a specific value, we just don’t know what it is. That value is for a specific characteristic (height). So, it’s a value that uses units relevant to the characteristic (such as CM).
For your example, the parameter is the proportion of faulty items. The actual parameter value is a proportion for the entire population. Of course, we’ll never know it exactly. You mention “5% of a batch.” Now that is a sample estimate of the parameter, not the parameter itself. Usually, the best we can do is estimate a parameter.
So, parameters are values but we never know those values exactly. However, we can estimate them.
I am trying to understand the importance of parameters in drawing conclusions when an exact value can be calculated. Can you explain this for me?
What are population parameters and how can they be use for estimation
Hi Musa,
This post answers your question. Read the section titled “Population Parameters versus Sample Statistics” more closely!
Dear Sir
Hope you are doing well, I want to ask a clarification when your time permit, please throw some light on it.
Which is the best way to estimate the (population) parameter?
1. Calculate the required sample size by defining Z-score (95%, 1-96), error (example 0, 03), and p (say .5 for maximum sample size) then estimate the sample statistic (example sample proportion). Then we say the calculated sample proportion is an unbiased estimator of the population proportion and 95% confidence the population proportion lies within plus or minus 0.03 (this value was used for calculating sample size) of the sample proportion. That is,
p- 0.03=< P <= p + 0.03
Or
We take a small sample (not calculate sample size statistically, say 40) due to limitation but using sampling techniques (srs, cluster or ..) while selecting a sample, then calculate the sample proportion after that and its variance (using statistical techniques). Finally, we say population proportion-P lies between p + – Z SE(p). That is,
p- Z[SE(p)] =< P <= p + Z [SE(p)]
Please clarify it, when your time permits.
Hi Lavan,
I’m not sure exactly what you’re asking. There are established power analysis methods for estimating samples sizes require to obtain statistical power that you specify. And other procedures for determining the precision of the estimate. For those types of procedures, you’ll need to enter information such as estimated effect size and estimated standard deviations. Read the post I link to for more information.
I hope this helps,
Jim
Content of this blog is awesome, quick absorb-able , Thank You
You’re very welcome, Sudarshan! I happy to hear that it was helpful!
Hello sir! I m always enjoying ur e-lectures. I hv a query. I m conducting research on gender based and type of school management based sample. Target population is secondary school students. I employed d probability sampling of randomization
Cud u tell me wheth i shud adopt straitified or simple random sampling technique m how. Remember d population is itself large but finite here