The Birthday Problem in statistics asks, how many people do you need in a group to have a 50% chance that at least two people will share a birthday? Go ahead and think about that for a moment. The answer surprises many people. We’ll get to that shortly.
In this post, I’ll not only answer the birthday paradox, but I’ll also show you how to calculate the probabilities for any size group, run a computer simulation of it, and explain why the answer to the Birthday Problem is so surprising.
Calculating Probabilities for the Birthday Problem
Many people guess 183 because that is half of all possible birthdays, which seems intuitive. Unfortunately, intuition doesn’t work well for solving this problem. So, let’s get straight to calculating probabilities for people sharing birthdays.
For these calculations, we’ll make a few assumptions. First, we’ll disregard leap year. That simplifies the math, and it doesn’t change the results by much. We’ll also assume that all birthdays have an equal probability of occurring and that they are independent events. The people already in the group don’t affect the probability of the next person’s birth date. Learn more about Independent Events.
Let’s start with one person, and then add people in one at a time to illustrate how the calculations work. For these calculations, it is easier to calculate the probability that no one shares a birthday. We’ll then take that probability and subtract it from one to derive the probability that at least two people share a birthday.
1 – Probability of no match = Probability of at least one match
For the first person, there are no birthdays already covered, which means that there is a 365/365 chance that there is not a shared birthday. That makes sense. We have just one person.
Now, let’s add in the second person. The first person covers one possible birthday, so the second person has a 364/365 chance of not sharing the same day. We need to multiply the probabilities of the first two people and subtract from one.
For the third person, the previous two people cover two dates. Hence, the third person has a probability of 363/365 for not sharing a birthday.
Now, you’re seeing the pattern for how to calculate the probability for a given number of people. Here’s the general form of the equation:
Related posts: Probability Fundamentals and Using the Multiplication Rule to Calculate Probabilities
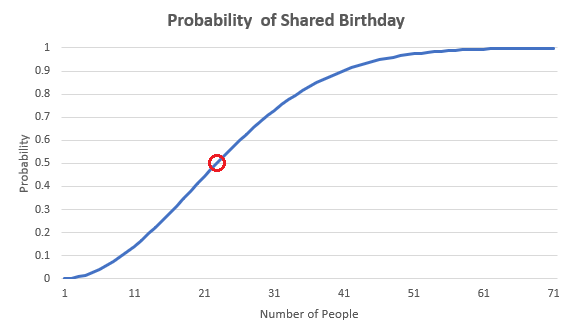
Graphing the Birthday Problem Probabilities
Using Excel, I can calculate and graph the probabilities for any size group. Download my Excel file: BirthdayProblem.
By assessing the probabilities, the answer to the Birthday Problem is that you need a group of 23 people to have a 50.73% chance of people sharing a birthday! Most people don’t expect the group to be that small. Also, notice on the chart that a group of 57 has a probability of 0.99. It’s virtually guaranteed!
Don’t worry. I’ll get to explaining this surprising result shortly. Let’s first verify the birthday problem answer of 23 using a different method.
Simulation of the Birthday Paradox
Using probability calculations, we expect a group of 23 people to have matching birthdays 50.73% of the time. Next, I’ll use a statistical simulation program to simulate the Birthday Paradox and determine whether the actual probabilities match the predicted probabilities. For this simulation, I’m using Statistics101, which is freeware.
The program comes with an example script that outputs the probability for a group of 25. I’ve modified their script so that it’ll collect 100,000 groups of 23 people and randomly assign a birthday to each person. The program determines whether birthdays match within each group of 23 and then calculates the percentage of those 100,000 groups that have a match. Based on the probability calculations, we’d expect about 50% of the groups to have matches. I’ll also have the program create a histogram of the number of matches within each group. Download my script: BirthdayProblem.
The simulation software found that 50.586% of the 100,000 groups had matching birthdays. That’s extremely close to the calculated probability of 50.73%. This simulation verifies the probability calculations.
The graph below shows the distribution of the number of matches in these groups of 23.
The furthest left bar indicates that 49.41% of the groups have no matches. The next bars show that 37% have one match, 11.4% have two, 1.9% have three, and 0.31% had more than three matches.
Why is the Group Size So Small for the Birthday Problem?
Like the Monty Hall Problem, most people think the answer to the Birthday Problem is surprising and it hurts their brain a bit! However, the answer is entirely correct, and we found it using two different methods—probability calculations and computer simulation. Let’s examine why the answer is counterintuitive.
Often people will think of their birthday and the probability that someone will match that specific date. However, the problem asks about any two individuals sharing a birthday. That means you have to compare all possible pairs of individuals. Assessing all pairs causes the number of comparisons to increase rapidly—and therein lies the source of confusion.
The formula for the number of comparisons between pairs of N people is: (N*(N-1))/2. As you can see in the table below, the number comparisons snowballs to 253 for only 23 people!
For sharing a birthday, each pair has a fixed probability of 0.0027 for matching. That’s low for just one pair. However, as the number of pairs increases rapidly, so does the probability of a match. With 23 people, you need to compare 253 pairs. With that many comparisons, it becomes difficult for none of the birthday pairs to match.
When there are 57 people, there are 1,596 pairs to compare, and it’s virtually guaranteed with a 0.99 probability that at least one pair will match birthdays.
I love problems like this where intuition leads you astray but math saves the day!
Because we’re talking about birthdays, can a statistician say that age is just a number?
I share the same birthday as an older brother of mine that I have not met. Same dad, different moms, both born on December 16th, about 14 years apart and only 3 min apart on birth time. I’m in an intro to statistics class now and I am terrible at math so your book has been helping. But class just started and I am having anxiety. This class is my only GER before I can go into the masters program.
I am aware of the counterintuitive nature of the “birthday problem” and often bring it up in meetings with 23 or more people… 🙂 I have a similar query that I have not been able to calculate adequately — any help gratefully appreciated. What is the probability that in a given group of N people (let’s say N=30 for the sake of simplicity) there will be TWO PAIRS of people who share the same birthday? And THREE PAIRS? And a given number of PAIRS? Thanks in advance.
The Birthday Problem is very interesting, which inspired me to apply your calculation to a real case. I kind of twist the truth (but the numbers are real) to keep the organization anonymous. Would you please take a look at my case: With 113 lottery tickets, there should be 6328 pairs of ticket numbers to compare, and the probability of each pair is 0.016%. Is my calculation correct, and what is the probability of getting 6 pairs in the 113 tickets ? Can I make a conclusion that the lottery ticket numbers are not printed randomly?
I introduced the Monte Hall Problem to my Algebra 1 students in high school. When I explained it I scaffolded the concept like this:
Instead of three doors, say there are 1 million doors. You get to choose one (only one is a winner), the other 999,999 have goats behind them. Monte Hall will open 999,998 doors to reveal goats, with one door and the one you selected being closed. Will you change now? All students said “YES”. I asked why and many agreed that the chance of picking right on the first time with 1,000,000 doors was “basically” zero that it would be dumb not to change. So then I would ask, what are your chances of picking right if there are only 3 doors? “33%” they said. Then I just looked at them and stared with a “well….?” kind of expression. That is when I got full buy in from the whole class at that point.
Love these types of problems. Wish there was a more discrete way to solve the birthday problem. We actually did that in a stats class in college. It was mind blowing when you see the answer, but the math checked out so I didn’t question it.
Thanks for your blog. The resources are great and the info is awesome too. Easy to navigate and use.
Hi Caesar,
Thanks for writing! I’ve found a similar thing that when you increase the number of doors, it helps students understand the solution better. If you read my post about the Monty Hall Problem, and look through the comments, you’ll see that idea pop up several times. Although, I think I must’ve been thinking too small because I usually use an example of 100 doors rather than 1 million! 🙂
I think it’s easier to understand the problem as a non-random process when Monty has to work through a larger number of doors. It’s basically a filtering process where by if the prize is in his set of doors, then it will be behind the final door he offers to the contestant. And, as you write, it emphasizes the point that you’re initial choice is almost certainly incorrect!
Thanks for the kind words about my website too! Very much appreciated!
Hello! So I have been trying to figure this problem out without using the method where you subtract each chance that they don’t share a birthday in order to find that they have a birthday. I managed to find and confirm that there are 253 combinations if there are 23 people, but I can not figure out how to use this number to get the 50%. I keep thinking that I’m supposed to take the chance that any two individuals share a birthday(1/365) and add that number to itself 253 times to get the answer, but when I do this I end up with 69%. Just wondering if there was a way to solve it like this. Thanks!
I have taught this (with betting) for many years to my college students. I (almost) always win. But I return the money at the end of the class for ethical reasons. This description by Jim, however, is the best I have seen. I also teach the “3-door” problem, but at least half of my students never accept the correct answer. Since I use these examples in my class lecture on Behavioral Finance, it makes my point perfectly: we are not wired for rationality, and certainly not for statistics. Kudos, Jim, for helping with the rewiring problem!
Hi Daniel,
Thanks so much for writing. I really appreciate your kind works. They made my day!
I’m always surprised by the number of people who refuse to accept the solution to the Monty Hall Problem. I’ve had many debates with people about the correct answer in the comments of my post on the topic!
How interesting… Made my day
I had a biometry professor who did this once in class. He had everyone write down their birthday on a piece of paper which someone collected and put them all in a bag. He actually made a bet with one of the students that at least two of the birthdays would be on the same day. As another student tallied all the birthdays, he went through the calculation on the chalkboard. He showed that the chance of a same-day birthday would have a very high chance of occurring with the number of people we had in the class. He said “with this many people, you can bet on it. You DID bet on it!” which drew some laughs. And sure enough, there were actually two pairs of students with the same birthday. And yes, the student handed over the money, which the professor kept.
Hi Jerry,
That’s a great story. I guess it pays to be knowledgeable in statistics! It could also make a great bar bet, as long as you had enough patrons in the bar!
Funny, thank Jim. Your study is wonderful…
yes, it is interesting. there are many situations where intuition ‘contradicts’ reality. On a slightly more advanced level, St. Petersburg paradox comes to mind.
Used it as an example in my Intro to Stats class!
This is great, thanks! I was on the right track for solving this with first calculating two people have a .0027 probability of the same birthday. For the third person I added the probability of two people to the probability of the third person matching one of the first two (1/363). However, it seems that these probabilities need to be multiplied, not added? Is there an intuitive way to explain that?
Very nice and interesting 👏👏
Interesting and cute !!!
Interesting information!